小学数学解题方法全解

方法概述

1.有些数学问题从正面入手求解比较繁琐、难度较大，如果打破思维常规，从问题的相反方面思考，往往能开拓解题思路、简化运算过程。这种解题方法叫做正难则反。

2.用正难则反解决问题分为正、逆运算转化和借助图形从条件的对立面去考虑两种情形。

（1）正、逆运算转化正、逆运算转化是指在解答数学题时，当从条件逼近结论有困难时，可以从结论出发，逆向出发，循着“要怎么，只要怎么”的思路，逐步沟通条件与结论，即通过条件、结论的“角色”转变，从结论逐步向条件靠拢以达到解决问题的目的。

（2）借助图形从条件的对立面考虑在解决一些数学问题时，可以从条件的对立面出发，利用图示法把不符合条件的情形求出来，进而求其符合条件的那个部分，从而将原问题解决。

典例精讲

方法点一 利用正、逆运算转化解决问题

例1 设1、3、9、27、81、243是6个给定的数，从这6个数中每次取1个或取几个不同的数求和（每个数只能取1次），可以得到1个新数，这样共得到63个新数，如果把它们从小到大依次排列起来是1、3、4、9、10、12……那么第60个数是多少？

方法指导

如果从正面（即从小到大）考虑，要算出第60个数较困难，如果调整思考方向，从大到小排列，问题即可解决。题中共得到63个新数，从小到大排列，第60个数恰好是从大到小排列的第4个数，由题知，第63个数为1+3+9+27+81+243=364，于是，第62个数应是364-1=363;第61个数是364-3=361;第60个数应是364-3-1=360，那么，第60个数是360。

正确解答

第63个数：1+3+9+27+81+243=364

第62个数：364-1=363

第61个数：364-3=361

第60个数：364-3-1=360

          答：第60个数是360。

例2 某市举行乒乓球比赛，有128名男选手参加单打比赛，比赛采取单场淘汰制，从开始比赛到决出冠军1名，一共需比赛多少场？

方法指导

解答这类问题的一般思路是每两人赛一场，第一轮要赛128÷2=64（场）；第二轮要赛64÷2=32（场）；第三轮要赛32÷2=16（场）……最后一轮决出冠军需2÷2=1（场）。故决出冠军共要比赛：128÷2+64÷2+32÷2+…+2÷2=64+32+16+…+2+1=127（场）。这样推算比较麻烦，如果变换思考角度，从结论想，就简单多了。

从结论想，只决出冠军1人，每场都淘汰1名运动员，共需淘汰（128-1）=127（名）运动员，这就要打127场，所以共要打127场。

正确解答

每场都淘汰1名运动员，一共淘汰128-1=127（名）运动员。即一共需比赛127场。

例3 1000个体积为1立方厘米的小正方体合在一起成为一个棱长为10厘米的大正方体，表面涂油漆后再分开为原来的小正方体，这些小正方体中至少有一面被油漆涂过的是多少个？

方法指导

此题从正面计数，根据正方体8个顶点，12条棱，6个面的特征，可以推算出来。但过程比较繁琐，且容易重数漏计。如果转换角度思考，从1000个中减去中间没涂的个数即可得到解答。

因为每条棱的长度是10厘米，去掉每两边的各1厘米，即得中间棱长为8厘米的正方体没有被刷到面。用小正方体的总个数减去中间的小正方体的个数，即可求出答案。

正确解答

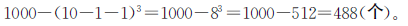
答：至少有一面被油漆涂过的是488个。

例4 将50拆分成10个质数之和，要求其中最大的质数尽可能大，那么最大的质数是多少？

方法指导

本题如果从正面着手，需要采用尝试调整法。即先写出一个较大的质数，再检验它是否符合题意。这样往往要尝试调整若干次才能得到正确的答案。如果从反面去想，要求其中最大的质数尽可能大，那么其他的质数就应该尽可能小。

最小的质数是2，如果9个质数都取2，则（50-2×9）=32不是质数。需调整为50-2×8-3×1=31。即这个最大质数是31。

正确解答

50-2×8-3×1=31

       答：最大的质数是31。

例5 在1、2、3……104、105中与105互质的数共有多少个？

方法指导

可用正难则反的策略，先想在1～105中与105不互质的数共有多少个，再从105中减去不互质的个数，即为所求答案。

因为105=3×5×7，所以与105不互质的自然数能被3或5或7整除。在1～105中，分别求出3、5、7的倍数的个数和3×5、5×7、3×5×7、3×7的倍数的个数，便可知在这105个数中与105不互质的数共有多少个。再求互质的数有多少个。

正确解答

3的倍数有105÷3=35（个）；

5的倍数有105÷5=21（个）；

7的倍数有105÷7=15（个）；

3×5=15的倍数有105÷15=7（个）；

5×7=35的倍数有105÷35=3（个）；

3×7=21的倍数有105÷21=5（个）；

3×5×7=105的倍数有1个。

与105不互质的数共有35+21+15-（7+5+3）+1=57（个）。

与105互质的数有105-57=48（个）

             答：与105互质的数共有48个。

方法点二 借助图形从条件的对立面考虑解决问题

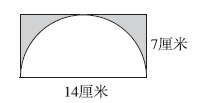
例6 如图，长方形的长为14厘米，宽为7厘米，求图中阴影部分的面积。

方法指导

阴影部分的面积为不规则图形，若从正面入手，无法求解，若从反面入手，把整个长方形看成一个整体，去掉空白部分就能求出阴影部分的面积。即阴影部分的面积=长方形的面积-空白半圆的面积。

正确解答
        

      答：阴影部分的面积为21.07平方厘米。

例7 正方体的6个面分别写着A、C、D、E、F、I,你能根据下图猜出与A、E、I相对的面分别是哪个面吗？

方法指导

根据正难则反的策略,首先从“与I相对的面不是哪一面”入手，从上图可知：与I相对的面不是A、E、F、C，只剩下D面，所以与I相对的面是D；同理与A相对的面不是I、D、E、F，只剩下C，所以与A相对的面是C；最后只剩下E面和F面，可知与E相对的面是F。

正确解答

与A相对的面是C，与E相对的面是F，与I相对的面是D。