第八章 整体思考法 - 本章内容
方法概述
1.整体思考法是指在研究某些数学问题时，往往不着眼于问题的各个组成部分，而是有意识地放大考察问题的“视角”，将需要解决的问题看作一个整体，通过研究问题的整体形式、整体结构或做种种整体处理后，达到顺利而又简洁地处理问题的目的。
2.用整体思考法解决问题分为“整体把握法”“整体替换法”“整体固定法”和“整体形变法”。
（1）整体把握法是指某些问题从表面上看需要局部求出各有关量，但从整体上把握这些量之间的关系，则思路会变得简洁清晰，解法更为巧妙。
（2）整体替换法是指在解决某些问题时，把一些组合式子视作一个“整体”，并把这个“整体”直接代入另一个式子，从而避免局部运算的麻烦和困难。
（3）整体固定法是指在解决问题的过程中，把所求式的值固定为一个字母以后，问题便转化为求这个字母的值。
（4）整体形变法就是将问题中的原图形（非规则图形或非特殊图形），经割补、平移或重组以后，转化成一个完整的特殊图形，让问题中的隐含条件显露出来，从而使问题得以解决。
典例精讲
方法点一 整体把握法
例1 一条马路长2000米，小张在马路的一端，小李在马路的另一端，他们分别从这条马路的两端同时出发，相对而行。小张每分钟走60米，小李每分钟走40米，小张带着一条狗，狗每分钟跑100米。这条狗与小张一同出发，碰到小李时就立刻回头向小张跑，碰到小张时又立即回头向小李跑，直到小张、小李相遇，这条狗从出发到小张、小李相遇，一共跑了多少米？
方法指导
解答本题从整体去考虑，两人与狗同时出发，同时相遇，所用的时间相同，即狗跑的时间就是两人相遇的时间：2000÷（60+40）=20（分），用这个时间乘狗跑的速度就得出狗跑的路程。
正确解答
100×[2000÷（60+40）]=2000（米）
答：一共跑了2000米。
例2 用1、2、3、5、7这五个数字可组成许多不同的五位数（每个五位数均由这五个数字组成），在这些五位数中质数有几个？
方法指导
解答本题从整体去考虑，不论怎样调换五个数字的位置，其数字和始终不变。这五个数字的和是1+2+3+5+7=18，而18能被3整除。因此，用1、2、3、5、7组成的五位数也一定能被3整除，所以不可能得到质数。即质数的个数为零。
正确解答
1+2+3+5+7=18
质数只有因数1和本身，而用这五个数字组成的五位数中都有因数3，所以这些五位数中没有质数。
例3 一项工程，甲、乙两队合作14天可以完成，两队合作6天后，余下的由乙队单独做还需16天。乙队单独完成该项工程需要多少天？
方法指导
解答本题从整体去考虑， 把14天的工作量看成14份，两队合作6天就完成了6份，还剩14 -6=8（份），乙队需要16天完成，从而完成每份需要16÷8=2（天），故完成全部工作14份，就需要2×14 =28（天）。
正确解答
16÷（14-6）×14=28（天）
答：乙队单独完成该项工程需要28天。
例4 搬运一个仓库的货物，甲需要10小时，乙需要12小时，丙需要15小时。有同样的仓库A和B，甲在A仓库，乙在B仓库同时开始搬运，丙帮助甲、乙搬运货物。最后两个仓库货物同时搬完，丙帮助甲、乙各多长时间？
方法指导
解答本题从整体去考虑，先求出甲、乙、丙3人完成总工作量的时间。无论丙帮甲、乙各搬运几小时，都是3人同时共搬完了2个单位“1”的工作量，所需时间是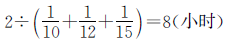
。甲8小时能完成
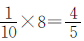，还需丙帮搬运
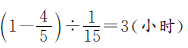，因此，丙帮助乙搬运8-3=5（小时）。
正确解答
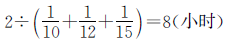
甲8小时能完成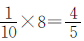
丙帮助甲：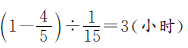
丙帮助乙：8-3=5（小时）
答：丙帮助甲3小时，帮助乙5小时。
例5 植树节六年级四个班参加植树，一班植树115棵，二班植树的棵数是其余三个班的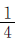
，三班植树的棵数是其余三个班的
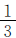，四班植树的棵数是其余三个班的
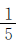，六年级四个班共植树多少棵？
方法指导
本题中同时有多个单位“1”的量，可以从整体上分析题意，把四个班植树的总棵数看作单位“1”，将条件变换说法，即二班植树的棵数是总棵数的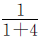
，三班植树的棵数是总棵数的
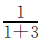，四班植树的棵数是总棵数的
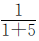，求四个班共植树的棵数就可迎刃而解了。
正确解答
把四个班植树的总棵数看作单位“1”。
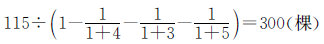
答：六年级四个班共植树300棵。
例6 有9只油桶，分别装油9、12、14、16、18、21、24、25、28千克，分给甲、乙两人各若干桶，最后只剩下1桶。已知甲分到的油是乙分到的油的2倍，剩下的这桶油有多少千克?
方法指导
解答本题可以从整体上把握，9桶油共重9+12+14+16+18+21+24+25+28=167（千克）。已知甲分到的油是乙分到的油的2倍，则甲、乙共分到的油的总量一定是3的倍数。而167÷3=55……2，那么剩下的那桶油的质量一定是被3除余2，符合条件的只能是重14千克的那桶油。
正确解答
9+12+14+16+18+21+24+25+28=167（千克）
167÷3=55……2
被3除余2，符合条件的只能是重14千克的那桶油。
例7 如下图，A、B是圆的直径的两端点，腾腾在A点，萍萍在B点同时出发相向而行，他们在C点第一次相遇，C点离A点80米；在D点第二次相遇，D点离B点60米，求这个圆的周长。
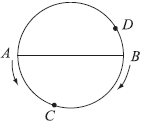
方法指导
解答本题从整体去考虑，第一次相遇时两人合走了半个周长，腾腾走了80米；第二次相遇时两人合走了一周半。因此，第二次相遇时两人合走的路程是第一次相遇时两人合走路程的3倍。那么，腾腾由A到D的路程应该是他从A到C的路程的3倍。求出AD的长，即得半圆的长。
正确解答
A到B的长（即半圆）为：80×3-60=180（米）
这个圆的周长：180×2=360（米）
答：这个圆的周长为360米。
方法点二 整体代换法
例8 计算。
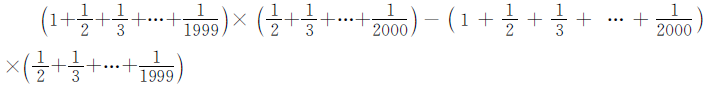
方法指导
此题按常规思维计算显然很繁琐，根据题中相同数据重复出现的特点，如果采用整体代换，就会化繁为简。
正确解答
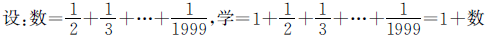
总结：整体代换是指在解决某些问题时，把一些组合式子视作一个“整体”，并把这个“整体”直接代入另一个式子，从而避免局部运算的麻烦和困难。
例9 下面的算式中，五个字母分别表示五个不同的数字，这五个字母各表示哪些数字时竖式成立？
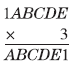
方法指导
这是一道数字谜题，分析尾数，从各位递推，获得答案比较繁琐。乘数和积中，都有相同的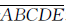
，如果整体想，将
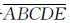看作一个整体，并设一个未知数代替ABCDE，用方程解，会使解题简便。
正确解答
解:设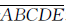=X
（100000+x）×3=x×10+1,x=42857
所以A=4，B=2，C=8，D=5，E=7。
当A=4，B=2，C=8，D=5，E=7时竖式成立。
方法点三 整体固定法
例10 有四个数，每次取3个求平均数，这样计算4次，依次得数为23、26、30、33，求这四个数的平均数。
方法指导
解答本题从整体考虑，就会很简单。假设这4个数分别是甲、乙、丙、丁。由每次取3个数求平均数后分别是23、26、30、33可知：
把这四个式子加在一起就得到：①+②+③+④=23+26+30+33=甲+乙+丙+丁，最后将甲、乙、丙、丁这4个数之和除以4就得到它们的平均数。
正确解答
（23+26+30+33）÷4=28
答：这四个数的平均数是28。
例11 有甲、乙、丙三种货物。买甲3件，乙7件，丙1件，共花去31.5元；买甲4件，乙10件，丙1件，共花去 42元。现在买甲、乙、丙各1件，需要花多少钱？
方法指导
解答本题时可以把甲、乙、丙各买1件的钱数看作一个整体数量。这样由已知条件可得：买甲3件，乙7件，丙1件，花31.5元①，买甲4件，乙10件，丙1件，花42元②。
要想求出买甲1件，乙1件，丙1件，共需花多少钱，必须使上述①与②中对应的“件数”相差1。
为此，可转化已知条件，将条件①中的每个量都扩大到原来的3倍，得到：买甲9件，乙21件，丙3件，花94.5元③。
将条件②中的每个量都扩大到原来的2倍，得到：买甲8件，乙20件，丙2件，花84元④。
③-④=买甲、乙、丙各一件共需要花的钱数。
正确解答
31.5×3=94.5（元）
42×2=84（元）
94.5-84=10.5（元）
答：现在买甲、乙、丙各1件，需要花10.5元。
方法点四 整体形变法
例12 如图一，四边形的周长是60厘米，点M到各边的距离都是4.5厘米，这个四边形的面积是多少平方厘米？
方法指导
解答本题从整体去考虑，因为四边形不是规则图形，要想求出总面积，必须转化成特殊图形，但这样做很麻烦，因此，我们要整体考虑。整体想，将四边形的周长（60厘米）看作四个三角形的底，点M到各边的距离（4.5厘米）看作高，如图二，则它的面积可巧解为60×4.5÷2=135（平方厘米）。
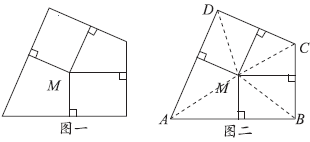
正确解答
连接AM、BM、CM、DM，如图二。四边形的面积=（AB+BC+CD+DA）×4.5÷2=60×4.5÷2=135（平方厘米）
答：这个四边形的面积是135平方厘米。
总结：所谓整体补形，就是将问题中的原图形（非规则图形或非特殊图形），经添加辅助线后转化成一个完整的特殊图形，让问题中的隐含条件显露出来，从而使问题获解。
例13 求下图中阴影部分的面积。
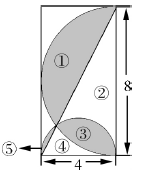
方法指导
解答本题从整体考虑，编号观图，整体列式，就会发现：
①+②+③=大半圆的面积
②+③+④=长方形面积的一半
③+④+⑤=小半圆的面积
阴影部分的面积：①+③+⑤
正确解答
因为：①+②+③=大半圆的面积=3.14 ×42÷2 =25.12（平方厘米）
②+③+④=长方形面积的一半=4×8÷2=16（平方厘米）
③+④+⑤=小半圆的面积=3.14×（4÷2）2÷2=6.28（平方厘米）
阴影部分的面积：①+③+⑤=25.12+6.28-16=15.4（平方厘米）