第六章 倒推法 - 本章内容
方法概述
1.有些数学问题，如果单单从已知条件去想，找出所求的结果，往往做起来很难。如果转变一下思考角度，从所叙述事情的最后结果出发，利用已知条件一步步逆向推理，逐步接近所求，直到解决问题，这种思考问题的方法，通常我们把它叫做倒推法，也叫逆推法或还原法。
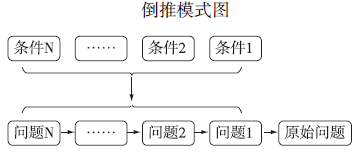
2.倒推法在实际解题中一般能从逆运算法、画图法、列表法三种方式入手。
（1）逆运算法还原类问题的解法通常是：怎样来的就怎样回去。也就是说，原来是加法，回过来是减法；原来是减法，回过来是加法；同样，原来是乘法，回过来是除法；原来是除法，回过来是乘法。如本书第86页例1（1）的题意分析图。
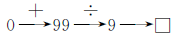
（2）画图法对于简单的每一次变化不太复杂的还原问题，可以直接列式一步步倒着推算，对于变化复杂的，可借助画图来帮助解决问题。如本书第87页例4的题意分析图。
（3）列表法在还原问题中，有些时候推理比较困难，我们通常可以借助列表法进行解决，然后按照解题步骤进行计算，解决问题变得容易些。如本书第89页例9的题意分析表格。
典例精讲
方法点一 运用逆运算倒推
例1 在下面各题的□里填上适当的数，使等式成立。
（1）□×9－99＝0
（2）45×2＋□÷3＝45×5
方法指导
（1）根据算式□×9－99＝0各部分数量之间的关系进行逆运算。
图示逆推过程：
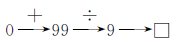
（2）根据算式45×2＋□÷3＝45×5各部分数量之间的关系进行逆运算。
图示逆推过程：
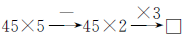
正确解答
（1）□=（0+99）÷9=11
（2）□=（45×5-45×2）×3=405
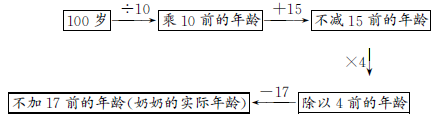
例2 李军问奶奶的年龄是多少，奶奶说：“把我的年龄加17，然后除以4，减15，再用10乘，恰巧是100岁。”李军奶奶的年龄是多少？
方法指导
100岁是通过加、除、减、乘后得到的，通过它们的逆运算方法，倒推回去，就能求出李军奶奶的实际年龄。
图示逆推过程：
正确解答
100÷10＝10（岁）
10＋15＝25（岁）
25 × 4＝100（岁）
100－17＝83（岁）
答：李军奶奶的年龄是83岁。
例3 小明在做一道加法算式题，由于粗心，将其中一个加数个位上的5看作9，十位上的8看作3，结果所得的和是123。正确的结果是多少？
方法指导
思路一 要求正确的结果，就要知道两个正确的加数。看错的加数是39，因此得到错误的和是123。根据逆运算可得到一个没看错的加数是123－39＝84，题中已知一个正确的加数是85，所以正确的和是85＋84＝169。
图示倒推过程：
思路二 把个位上的5看作9，相当于把正确的结果多算了4，求正确的结果应把4减去；把十位上的8看作3，相当于把正确的结果少算了50，求正确的结果应把50加上。这样，正确的结果是123＋50－4＝169。
图示倒推过程：
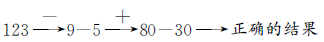
正确解答
解法一 123－39＋85
＝84＋85
＝169
解法二 9－5＝4
80－30＝50
123＋50－4＝169
答：正确的结果是169。
方法点二 画图倒推
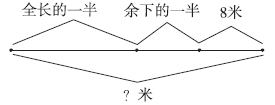
例4 花园要铺一条甬路，第一天铺了一半，第二天又铺了余下的一半，还剩8米。这条甬路全长多少米？
方法指导
本题中找准最后剩余的米数与每天铺后余下的米数之间的关系，通过画线段图来理解题意。
图示逆推过程：
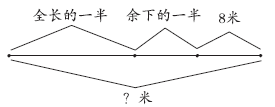
从上面的线段图可以看出：剩下的8米和余下的一半同样多，那么全长的一半是：8×2=16（米），全长：16×2=32（米）。
正确解答
8×2=16（米）16×2=32（米）
答：这条甬路全长32米。
例5 高原收集了许多画片，他送给小明画片总数的一半多10张，然后又送给小红剩下的一半还多10张，最后还剩65张。高原原来有多少张画片？
方法指导
题中数量关系看起来很复杂，只要找准问题的切入点，借助画图法来理解题意即可。
图示逆推过程：
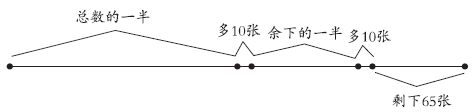
从上图可以看出， 最后剩下的65张画片加上10张正好是余下的一半，余下的一半为65+10=75（张），所以第二次送出后余下75×2=150（张）；150张加上10张就是总数的一半，所以第一次送出总数的一半是150+10=160（张），总数为160×2=320（张）。
正确解答
65+10=75（张）75×2=150（张）
150+10=160（张）160×2=320（张）
答：高原原来有320张画片。
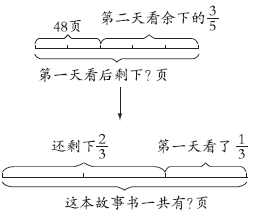
例6 一本故事书，小明第一天看了全书的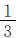
，第二天看了余下的
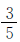，还剩下48页，这本书共有多少页？
方法指导
从“剩下48页”入手倒着往前推，它占余下的1－＝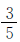
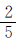。第一天看后还剩下48÷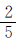＝120（页），这120页占全书的1－＝
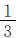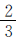，这本书共有120÷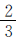＝180（页）。
正确解答 48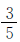÷1－÷1－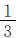
＝120÷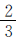
＝180（页）
答：这本书共有180页。
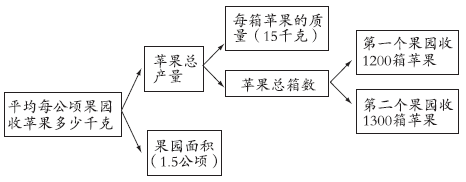
例7 某农场有两个果园,共1.5公顷。第一个果园收苹果1200箱，第二个果园收苹果1300箱，每箱苹果重15千克。平均每公顷果园收苹果多少千克？
方法指导
从问题出发，逆推回去，找到解决问题的办法。要求每公顷果园产量，必须知道苹果的总产量和果园的总面积 （1.5公顷）；要求出苹果的总产量，必须知道每箱的质量（15千克）和总箱数；要求总箱数，必须知道第一个果园收的箱数（1200箱）和第二个果园收的箱数（1300箱），这些都是已知条件。
图示逆推过程：
正确解答 （1200+1300）×15÷1.5
=2500×15÷1.5
=37500÷1.5
=25000（千克）
答： 平均每公顷果园收苹果25000千克。
方法点三 列表倒推
例8 一种昆虫，由幼虫到成虫，每天长大一倍，15天能长到40毫米。这种昆虫长到5毫米时，需要多少天？
方法指导
根据这种昆虫“每天长大一倍”，由“15天能长到40毫米” 列表从后往前推导就能发现答案。
正确解答
14天：40÷2=20（毫米）
13天：20÷2=10（毫米）
12天：10÷2=5（毫米）
答：这种昆虫长到5毫米时，需要12天。
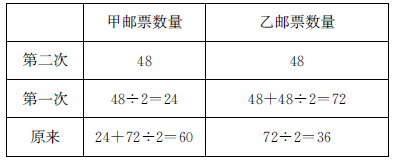
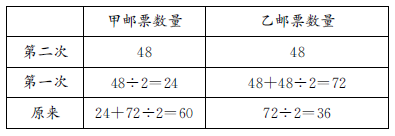
例9 甲、乙两人有若干枚邮票，如果甲拿出和乙同样多的邮票给乙，乙再拿出和甲同样多的邮票给甲，这时两人都是48枚邮票，那么甲、乙两人原来有多少枚邮票？
方法指导
借助表格从后往前推导：
正确解答
48÷2=24（枚）48+48÷2=72（枚）
乙原来的邮票：72÷2=36（枚）
甲原来的邮票：24+72÷2=60（枚）
答：乙原来有36枚邮票，甲原来有60枚邮票。
例10 甲、乙、丙、丁四人各有若干枚棋子，甲先拿出自己棋子的一部分分给乙、丙两人，使他们的棋子数量各增加一倍；随后，乙也将自己棋子的一部分以同样的方式分给丙、丁两人，使他们的棋子数量也各增加一倍；然后，丙也将自己棋子的一部分以这样的方式分给了甲、丁两人；最后，丁也用这样的方式把自己的棋子给了甲、乙。这时四人的棋子数量相同，每人有16枚。原来甲、乙、丙、丁四人各有多少枚棋子？
方法指导
这道题看起来非常长，也非常复杂。但可以通过列表来解决。最后一次数量改变后，四人的棋子数量都是16枚，然而在每次变化中，有一人的棋子数量是不会改变的。有两人的棋子数量会增加一倍，倒推、还原的时候，应该除以2。而另外一人的棋子数量减少了两人增加的棋子总数，还原时需要加上这个数量。
可以列出这样一张表格来解答这道题：
正确解答
甲原来有30枚棋子；
乙原来有17枚棋子；
丙原来有9枚棋子；
丁原来有8枚棋子。