第五章 假设法 - 本章内容
方法概述
1.假设法就是在解决问题的过程中,遇到一些条件少,无法下手的题目,根据题目中的已知条件或结论作出某种假设,把复杂的问题转化为简单的问题处理,然后再进行推算,以求出原题的答案。
2.假设法的种类:
(1)条件假设法在解应用题时,有些数量关系比较隐蔽,如果对条件作出某种假设,则往往能顺利地找到解题途径。
(2)结果假设法当直接解一些应用题似乎无从下手时,可对问题的结果提出假设性答案,然后进行推算,当所得的结果与题目的条件出现差错时,再进行调整直至与题目的条件符合,从而得出正确的答案。
(3)过程假设法有些应用题过程比较复杂,数量关系不明显,这时,可对过程进行适当假设,使隐蔽的数量关系明朗化,达到化难为易的目的。
典例精讲
方法点一 条件假设法
例1 如果A×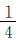 =B×
=B×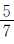 =C×
=C×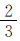 ,且A、B、C均不为0,请把A、B、C按从大到小的顺序排列。
,且A、B、C均不为0,请把A、B、C按从大到小的顺序排列。
方法指导
假设A×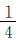 =B×
=B×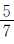 =C×
=C×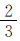 =1,则A与
=1,则A与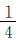 ,B与
,B与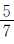 ,C与
,C与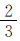 分别互为倒数,由此可以得出:A=4,B=
分别互为倒数,由此可以得出:A=4,B=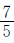 ,C=
,C=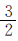 。最后比较这三个数的大小是:4>
。最后比较这三个数的大小是:4>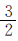 >
>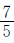 ,即,A>C>B。
,即,A>C>B。
正确解答 A>C>B
例2 一台笔记本电脑,先提价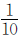 ,再打九折出售。现价和原价进行比较,( )。
,再打九折出售。现价和原价进行比较,( )。
A.现价贵 B.原价贵 C.价格没有变化 D.无法判定
方法指导
假设这台电脑4000元,提价后的电脑售价4000×1+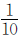 =4400(元),现价是在4400元的基础之上打九折,现价就是4400×90%=3960(元)。最后比较4000和3960的大小。
=4400(元),现价是在4400元的基础之上打九折,现价就是4400×90%=3960(元)。最后比较4000和3960的大小。
正确解答 B
例3 小明上山的速度是每小时4千米,到了山顶后,小明按照原路返回,平均每小时行6千米,求小明上下山的平均速度。
方法指导
假设山脚到山顶的路程是12千米,则小明的上山时间为12÷4=3(小时),下山的时间为12÷6=2(小时),用小明上下山的路程和12×2=24(千米)除以上下山的时间和,就可以求出小明上下山的平均速度。
正确解答
假设山脚到山顶的路程是12千米,则小明上山时间为12÷4=3(小时),下山时间为12÷6=2(小时)。
平均速度:12×2÷(3+2)=4.8(千米/时)
答:小明上下山的平均速度是4.8千米/时。
提示:假设山脚到山顶的路程时,把这段路程假设成上山和下山速度的公倍数,计算起来比较简便。
例4 甲管注水速度是乙管的1.5倍,同时开放甲、乙两个水管向游泳池注水,12小时可注满。现在先开甲管向游泳池注水若干小时,剩下的由乙管注9小时将游泳池注满,问甲管注水时间是多少。
方法指导
假设乙管每小时注水1吨,则甲管每小时注水1×1.5=1.5(吨),两个水管12小时共注水(1+1.5)×12=30(吨),即注满游泳池要用30吨水。乙管9小时注1×9=9(吨),余下的30-9=21(吨)由甲管注水,需要注21÷1.5=14(小时)。
正确解答
假设乙管每小时注水1吨,则甲管每小时注水1×1.5=1.5(吨)。
(1+1.5)×12=30(吨)1×9=9(吨)30-9=21(吨)
21÷1.5=14(小时)
答:甲管注水时间是14小时。
例5 电影票10元一张,降价后观众增加一倍,收入将增加五分之一,那么一张电影票降低了多少元?
方法指导
这道题没有告诉降价前的观众人数是多少,用常规思路势必受阻。为了使常规思路畅通无阻,要设具体数量,不妨想最简单的。假设降价前只有1人购票,则按原价可收入10元,降价后人数为1+1=2(人),收入为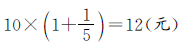 ,因此,一张电影票降价10-12÷2=4(元)。
,因此,一张电影票降价10-12÷2=4(元)。
正确解答假设降价前只有1人购票,则按原价可收入10元,降价后的人数是1+1=2(人),降价后的收入是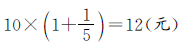 ,每张电影票降价的钱数是10-12÷2=4(元)。
,每张电影票降价的钱数是10-12÷2=4(元)。
答:一张电影票降低了4元。
提示:在不改变原有数量关系的前提下,假设其为最简单情况,可使问题得到简化,易于求解。
例6 猎狗发现在离它10米远的前方有一只奔跑的兔子,马上紧追上去,兔跑9步的路程,猎狗只需跑5步,但猎狗跑2步的时间兔子却跑3步,问猎狗追上兔子时共跑了多少米。
方法指导
猎狗和兔子每步跑的距离以及每步用时都是未知条件,可依据二者的数量关系对其进行假设。假设猎狗每步跑1米,每步用1秒钟,则兔子每步跑1×5÷9=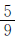 (米),每步用1×2÷3=
(米),每步用1×2÷3=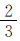 (秒),兔子的速度是每秒跑
(秒),兔子的速度是每秒跑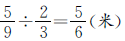 ,猎狗追上兔子的时间为
,猎狗追上兔子的时间为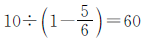 (秒),猎狗共跑了1×60=60(米)。
(秒),猎狗共跑了1×60=60(米)。
正确解答
假设猎狗每步跑1米,每步用1秒钟。
则兔子每步跑的路程:1×5÷9=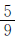 (米)
(米)
每步用时:1×2÷3=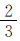 (秒)
(秒)
兔子的速度: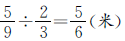
猎狗追上兔子的时间: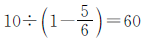 (秒)
(秒)
猎狗跑的路程:1×60=60(米)
答:猎狗追上兔子时共跑了60米。
方法点二 结果假设法
例7 同学们参加野营活动,李军到负责后勤的老师那里去领碗,老师问他领多少,他说领55个。又问:“多少人吃饭?”他说:“一人一个饭碗,两人一个菜碗,三人一个汤碗。”算一算,有多少个同学参加野营活动?
方法指导
假设参加野营的同学有6人(1,2,3的最小公倍数)。6个人共需要的碗数为6÷1+6÷2+6÷3=11(个)。李军实际领55个碗,55÷11=5,是假设6人所领碗数的5倍,所以参加野营的同学数也是假设人数的5倍。
正确解答
假设参加野营的同学有6人。
6个人需要的碗数:6÷1+6÷2+6÷3=11(个)
参加野营活动的同学:6×(55÷11)=30(个)
答:有30个同学参加野营活动。
例8 笼中共有鸡兔100只,350只脚,问鸡兔各有多少只?
方法指导
思路一 假设100只全为兔,则应有4×100=400(只)脚,比实际多了400-350=50(只)脚,如果把一只兔换成一只鸡,那么可减少4-2=2(只)脚,要减少50只脚,就要换50÷2=25(只)鸡,这样就求出了鸡的只数。
思路二 假设100只全为鸡,则应有2×100=200(只)脚,比实际少了350-200=150(只)脚,如果把一只鸡换成一只兔,那么可增加4-2=2(只)脚,要增加150只脚,就要换150÷2=75(只)兔,这样就求出了兔的只数。
正确解答
方法一 鸡:(4×100-350)÷(4-2)=25(只)
兔:100-25=75(只)
方法二 兔:(350-2×100)÷(4-2)=75(只)
鸡:100-75=25(只)
答:鸡有25只,兔有75只。
总结: 
例9 甲、乙、丙、丁四个人参加数学竞赛,赛后他们四人预测名次如下:
(1)甲说:“丙第一,我第三。”
(2)乙说:“我第一,丁第四。”
(3)丙说:“丁第二,我第三。”
(4)丁没有说话。
最后公布结果时,发现他们每人都预测对了一半,请说出他们四人竞赛的名次。
方法指导
先假设甲说丙为第一是正确的,那么甲为第三是错误的。
根据(2)可知,乙为第一是错误的,那么丁为第四是正确的。
根据(3)可知,丁为第二是错误的,那么丙为第三是正确的。
这样,丙为第一和丙为第三相互矛盾。所以,甲说丙为第一是错误。
丙为第一是错误的,那么甲为第三是正确的。
根据(3)可知,丙为第三是错误的,那么丁为第二是正确的。
根据(2)可知,丁为第四是错误的,那么乙为第一是正确的。
所以,乙为第一,丁为第二,甲为第三,丙为第四。
正确解答
乙为第一,丁为第二,甲为第三,丙为第四。
总结:每人说的两句话中,一句对一句错是分析解决这道题的关键,解决这个问题的方法是:先作出假设,然后根据已知条件进行正确的推理。如果推出矛盾,则说明假设不合理。没有推出矛盾,则说明假设合理。
方法点三 过程假设法
例10 买语文书30本,数学书24本,共花406.2元,已知每本语文书比每本数学书贵2.2元,语文书每本多少元?数学书每本多少元?
方法指导
假设语文书的单价便宜2.2元,那么数学书和语文书的单价就相同了。买30本语文书就可便宜2.2×30=66(元)。406.2元减去66元所得的差正好是30+24=54(本)数学书的总价。这样就可以求出数学书的单价了。
正确解答
数学书的单价:(406.2-2.2×30)÷(30+24)
=340.2÷54
=6.3(元)
语文书的单价:6.3+2.2=8.5(元)
答:语文书每本8.5元,数学书每本6.3元。
例11 少年宫开办音乐、美术两个培训班,去年共招收200人。今年计划招收246人,其中今年音乐班招收人数比去年增加25%,美术班招收人数比去年增加20%。今年计划招收的音乐班、美术班各有多少人?
方法指导
假设美术班今年比去年也增加25%,则今年计划招收200×(1+25%)=250(人),比实际多250-246=4(人),这是因为美术班今年比去年增加的百分比与实际相比较多了去年的25%-20%=5%,去年美术班的5%对应的是4人,因此,去年美术班有4÷5%=80(人)。
正确解答
去年美术班人数:[200×(1+25%)-246]÷(25%-20%)
=(250-246)÷5%
=80(人)
今年美术班人数:80×(1+20%)
=80×120%
=96(人)
今年音乐班人数:246-96=150(人)
答:今年音乐班计划招收150人,美术班计划招收96人。