第三章 方程法 - 本章内容
方法概述
1.方程法。方程法就是在解决问题时，让未知量与已知量处于同样的地位，即把未知量当作一个已知量看待，然后根据题中已知量和未知量之间存在的等量关系，列出相应的方程，最终求未知量是多少。
2.列方程解决问题的步骤。
（1）审题，弄清题意。即全面分析已知数与已知数及已知数与未知数之间的关系，特别要把牵涉到的一些概念术语弄清，如同向，相向，增加到，增加了等；
（2）引进未知数。用x表示所求的数量或有关的未知量。在小学阶段所遇到的应用题并不十分复杂，一般只需要直接把要求的数量设为未知数；
（3）找出应用题中数量间的相等关系，列出方程；
（4）解方程，找出未知数的值；
（5）检验并写出答案。检验时，一是要将所求得的未知数的值代入原方程，检验方程的解是否正确；二是检查所求得的未知数的值是否符合题意，不符合题意的要舍去，保留符合题意的解。
典例精讲
方法点一 利用几何图形的周长、面积和体积计算公式列方程
例1 一个三角形的面积是200平方厘米，它的底是25厘米，高是多少厘米？
方法指导
本题是关于三角形面积计算问题。解此题首先要根据三角形的面积计算公式“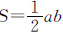
”列出等量关系式，然后设所求问题高为x厘米，即可列出方程解答。
正确解答
解：设高是x厘米。
25x÷2＝200
25x＝200×2
x＝400÷25
x＝16
答：高是16厘米。
例2 一个圆的周长是18.84分米，那么这个圆的面积是多少？
方法指导
本题是根据圆的周长计算圆的面积问题，要先求出圆的半径，再计算圆的面积。计算圆的半径时，根据圆的周长公式“C=2πr”列出等量关系式，设半径为x分米，即可列出方程解答。
正确解答
解：设圆的半径是x分米。
2×3.14x＝18.84
6.28x＝18.84
x＝18.84÷6.28
x＝3
面积：3.14×32=28.26（平方分米）
答：这个圆的面积是28.26平方分米。
总结:列方程解决问题时，当直接设所求问题为未知数不易列出方程时，可以设与所求问题相关的量为未知数。
例3 一个圆锥形的稻谷堆，底面半径是6米，高0.5米，把这堆稻谷装进一个圆柱形粮仓，正好装满，这个粮仓里面的底面直径为4米，高是多少米？
方法指导
本题是关于圆锥和圆柱的体积相互转化问题。根据“圆柱的体积=圆锥的体积”列出等量关系式，然后设所求问题圆柱的高是x米。就可以列出方程解答。
正确解答
解：设高是x米。
方法点二 利用数量关系列方程
例4 甲、乙两辆汽车从相距660千米的两地相向而行，6小时相遇，若甲车比乙车每小时多行10千米，则乙车的速度是多少？
方法指导
思路一 本题是关于两车相遇的行程问题，可以根据“速度和（甲速+乙速）×相遇时间＝总路程”列出等量关系式，然后设所求问题乙的速度为x千米/时，即可列出方程解答。
思路二 本题还可以根据“甲车行驶的路程+乙车行驶的路程=总路程”列出等量关系式，在表示甲、乙两车行驶的路程时，设所求问题乙车的速度为x千米/时，乙车行驶的路程表示为6x,甲车行驶的路程表示为6（x+10）。
正确解答
解法一 解：设乙车的速度为x千米/时。
（x+10+x）×6＝660
2x+10＝110
2x＝100
x＝50
解法二 解：设乙车的速度为x千米／时。
6x+6（x+10）＝660
12x+60＝660
12x＝600
x＝50
答：乙车的速度是50千米／时。
例5 甲车间有280人，乙车间有50人，要使乙车间的人数是甲车间的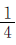
，需从甲车间调入乙车间多少人？
方法指导
根据调配后“乙车间的人数是甲车间的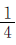”可以列出等量关系式，即“调配后甲车间的人数×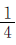=调配后乙车间的人数”。设从甲车间调入乙车间x人，则调配后甲车间为（280-x）人，乙车间为（50+x）人。
正确解答
解：需从甲车间调入乙车间x人。
（280-x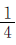）×=50+x
280-x=200+4x
5x=80
x=16
答：需从甲车间调入乙车间16人。
例6 一个两位数，十位数字是个位数字的3倍，若把这个两位数的十位数字和个位数字对调，得到的新数比原来少36，求这个两位数。
方法指导
本题可以根据这个两位数的十位数字和个位数字对调前后的数量差列出等量关系式，即“原数-新数=36”。设原来这个两位数个位上的数字为x,则十位上的数字为3x,原数就可以表示为“3x×10+x”；新数就可以表示为“10×x+3x”。
正确解答
解：设这个两位数个位上的数字为x，则十位上的数字为3x。
3x×10+x-（10×x+3x）＝36
31x-13x＝36
18x＝36
x＝2
十位上的数字：3×2＝6
答：这个两位数是62。
总结:列方程解答问题时，如果题中的两个量都可以设为未知数，且两个量存在倍数关系，一般设1倍量为未知数计算起来比较简便。
例7 红气球和黄气球一共有38个，其中红气球的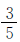
等于黄气球的
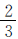。红气球和黄气球各有多少个？
方法指导
根据题中“红气球的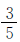等于黄气球的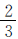”列出等量关系式，即红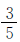气球×=黄气球×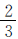。设其中一种气球的数量为x个,则另一种气球的数量为（38-x）个。
正确解答
解法一 解:设黄气球有x个。
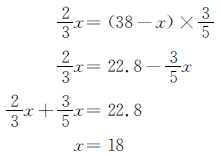
红气球：38-18=20（个）
解法二 解:设红气球有x个。
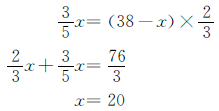
黄气球：38-20=18（个）
答：红气球有20个，黄气球有18个。
例8 某校六年级男生人数占总人数的54％，转入3名女生，转走3名男生后，这时女生人数占总人数的48％。现在有男生多少人？
方法指导
转进与转出的人数相同，所以六年级的总人数不变。可以根据六年级男生人数的变化列出等量关系式，即“六年级总人数的54％-转走3人=六年级总人数的（1-48%）”，也可以根据六年级女生人数的变化列出等量关系式，即“六年级总人数的（1-54％）+转入3人=六年级总人数的48%”。
正确解答
解:设六年级的总人数为x人。
x×54％-3=x×（1-48%）
0.54x-0.52x=3
x=3÷0.02
x=150
男生人数：150×54％-3=78（人）
答：现在有男生78人。
例9 用浓度分别分75%和25%的两种药液配制浓度为45%的药液900毫升，这两种药液各需多少毫升？
方法指导
题中配制前两种药液中药的含量与配制成浓度为45%后药液中药的含量是相等的，根据“浓度为75%的药液中药的含量+浓度为25%的药液中药的含量=900毫升浓度为45%的药液中药的含量”列出等量关系式。设需要浓度为75%的药液x毫升，则需浓度为25%的药液（900-x）毫升。
正确解答
解：设需要浓度为75%的药液x毫升。
75%x+25%×（900-x）＝45%×900
75%x－25%x＝900×45%－900×25%
0.5x＝180
x＝360
25%的药液:900－360＝540（毫升）
答：需要浓度为75%的药液360毫升，浓度为25%的药液540毫升。
例10 某商品若按标价的90%出售，则可以获利30元；若按标价的70%出售，则要亏损20元，该商品进价和标价各是多少元？
方法指导
本题要根据商品进价不变列出等量关系式，题中存在的等量关系为：商品标价的90%-30=商品标价的70%+20。设该商品的标价为x元,求出标价后，再根据“标价的90%-30”或“标价的70%+20”求出进价。
正确解答
解：设该商品的标价为x元。
90%x－30=70%x+20
0.2x=50
x=250
进价：90%×250-30＝195（元）
答：商品的进价是195元，标价是250元。
例11 从下午4点开始，再经过多少分钟时针与分针重合？
方法指导
分针一分钟走1格，时针一分钟走1〖〗12格，下午4时，分针落后时针20格。分针与时针重合，就是分针要比时针多走20格，即“分针行走的格子数-时针走的格子数=20格”，根据这个等量关系可以列出方程。
正确解答
解：设再经过x分钟时针与分针重合。
例12 鸡兔同笼，头共26个，脚共66只，求鸡与兔各有多少只。
方法指导
本题是鸡兔同笼问题，可以根据“鸡的脚数+兔的脚数=66只”列出等量关系式，设其中一种动物的数量为x只，则另一种动物的数量为（26-x）只。
正确解答
解法一 解：设鸡有x只，则兔有（26-x）只。
2x+（26-x）×4=66
x=19
兔：26-19=7（只）
解法二 解：设兔有x只，则鸡有（26-x）只。
4x+（26-x）×2=66
x=7
鸡：26-7=19（只）
答：鸡有19只，兔有7只。