第二章 转化法 - 第3讲 单位“1”的转化
方法概述
1.单位“1”的转化是指在解答有关分数的实际问题时，题中同时存在多个单位“1”，根据解决问题的需要，把不同的单位“1”转化成统一的单位“1”，使隐蔽的数量关系明朗化的解题方法。
2.常用的转化单位“1”的方法。
（1）画图转化。
（2）列表转化。
（3）利用不变量转化。
（4）用倍比关系转化。
（5）用条件转化法转化。
典例精讲
方法点一 画图转化单位“1”
例1 乙数是甲数的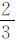
，丙数是乙数的
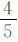，丙数是甲数的几分之几？
方法指导
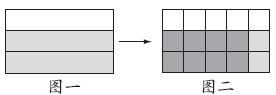
可以用画格子图法理解甲数和丙数的关系。如图，把甲数看作一个整体，用长方形表示。把长方形平均分成3份，乙数占其中的2份，如图一所示。再把阴影部分平均分成5份，丙数占其中的4份，如图二所示。从图中可以看出，丙数是甲数的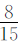
。
正确解答
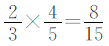
答：丙数是甲数的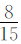
。
例2 某工程队计划修一条长800米的水渠，第一周修了全长的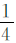
，第二周修的相当于第一周的
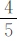，第二周修了多少米？
方法指导
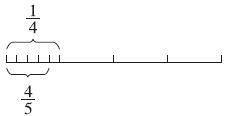
观察下图可以发现，第二周修的水渠长度是这条水渠全长的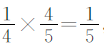
，用水渠的总长800乘
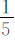即可求出第二周修的水渠长度。
正确解答
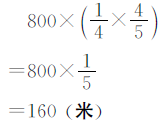
答：第二周修了160米。
方法点二 列表转化单位“1”
例3 甲数是乙数的
，乙数是丙数的
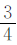，甲、乙、丙三个数的和是216，甲、乙、丙三个数各是多少？
方法指导
解这道题的关键是确定谁是单位“1”，然后判断216里有几个单位“1”。
思路一 把丙数看作单位“1”。
思路二 把乙数看作单位“1”
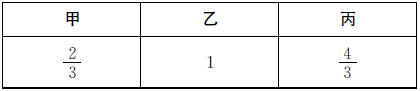
思路三 把甲数看作单位“1”。
正确解答
解法一
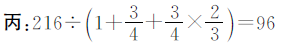
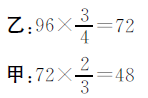
解法二
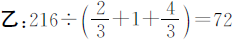
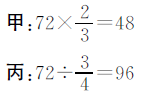
解法三
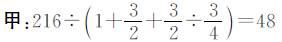
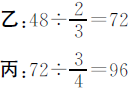
答：甲数是48，乙数是72，丙数是96。
例4 已知甲校学生数是乙校学生数的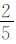
，甲校的女生数是甲校学生数的
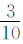，乙校的男生数是乙校学生数的
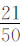，那么两校女生总数占两校学生总数的几分之几?
方法指导
思路一 把乙校学生数看作单位“1”。
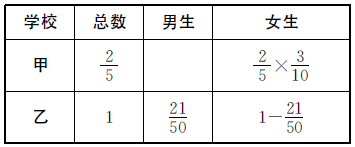
思路二 把甲校学生数看作单位“1”。
观察上表可知，两校的女生总数可以用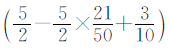
表示，两校的总人数可以用
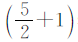表示，用
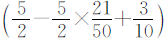除以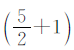
，即可求出两校女生总数占两校学生总数的几分之几。
正确解答
解法一
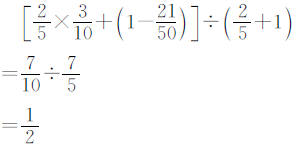
解法二
答：两校女生总数占两校学生总数的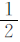
。
方法点三 利用不变量转化单位“1”
例5 有两筐橘子，乙筐橘子质量是甲筐的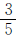
，从甲筐取出5千克橘子放入乙筐后，乙筐的橘子质量是甲筐的
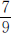。甲、乙两筐橘子共重多少千克？
方法指导
根据已知条件“从甲筐取出5千克橘子放入乙筐后”，可以知道甲、乙两筐橘子的数量都发生了变化，但是甲、乙两筐橘子的总质量没有发生变化。把两筐橘子的总质量看作单位“1”，则原来甲筐里的橘子占这两筐橘子总质量的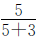
，取出5千克橘子后，甲筐里剩下的橘子占这两筐橘子总质量的
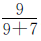。由此得出： 5千克橘子相当于两筐橘子总质量的
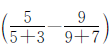7，用5除以
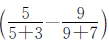就得到这两筐橘子的总质量。
正确解答
答：甲、乙两筐橘子共重80千克。
例6 某校六年级，如果增加2名男生，女生人数则是男生人数的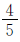
。如果减少3名男生，女生人数则是男生人数的
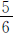。这个学校六年级男、女生原来各有多少人？
方法指导
题中女生人数是一个不变量，把它看作单位“1”，则增加2名男生后的男生人数是女生人数的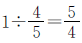
，减少3名男生后的男生人数是女生人数的
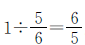。两种情况男生相差2+3=5（人），这5人对应的分率是
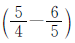，因此这个学校六年级女生原来有
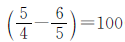（人），则男生原来有
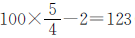（人）。
正确解答
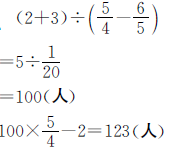
答：这个学校六年级男生原来有123人，女生原来有100人。
例7甲、乙、丙、丁四个工程队合修一条路，结果甲队修了另外三队总数的一半，乙队修了另外三队总数的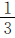
，丙队修了另外三队总数的
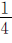，丁队修了910米，这条路全长多少米？
方法指导
这条路的总长是不变的量，把这条路的全长看作单位“1”，根据“甲队修了另外三队总数的一半”可知，甲队修了这条路的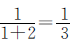
；同理，乙队修了全长的
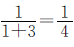，丙队修了全长的
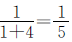。丁队修的910米是这条路总长的
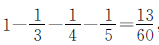，用910米除以
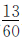就可以求出这条路的全长。
正确解答
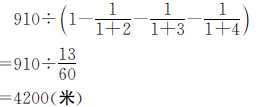
答：这条路全长4200米。
方法点四 用倍比关系转化单位“1”
例8 有120个皮球，分给两个班使用，一班分到的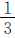
与二班分到的
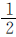相等，求两个班各分到多少个皮球。
方法指导
思路一 把二班分到的皮球数看作单位“1”。
根据“一班分到的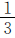
与二班分到的
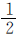相等”可知，一班的“1”中有几个
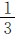，就有几个二班的
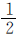，这样一班分到的皮球数就相当于二班的
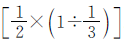。两个班分到的皮球数可以用二班分到皮球数量的
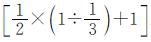来表示，用皮球总数120除以
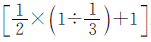就可以求出二班分到多少个皮球，然后求出一班分到多少个皮球。
思路二 把一班分到的皮球数看作单位“1”。
根据“一班分到的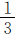
与二班分到的
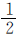相等”可知，二班的“1”中有几个
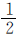，就有几个一班的
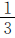，这样二班分到的皮球数就相当于一班的
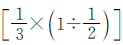。两个班分到的皮球数可以用一班分到皮球数量的
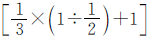来表示。用皮球总数120除以
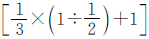就可以求出一班分到多少个皮球，然后求出二班分到多少个皮球。
正确解答
解法一
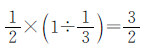
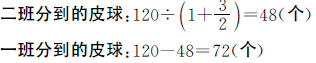
解法二
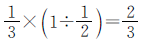
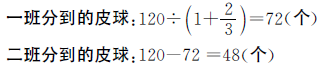
答：一班分到72个皮球，二班分到48个皮球。
例9 甲、乙两数相差30，其中甲数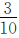的
与乙数的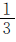
相等，求这两个数的和是多少。
方法指导
思路一 把甲数看作单位“1”。
根据“甲数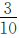的
与乙数的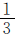
相等”可知，乙数里有几个
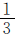就有几个甲数的
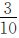，即乙数是甲数的
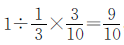，由此得出：两数的差30对应的是甲数的
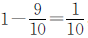，用甲、乙两数的差30除以
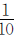就能求出甲数，然后求出乙数。
思路二 把乙数看作单位“1”。
根据“甲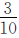数的
与乙数的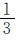
相等”可知，甲数里有几个
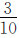就有几个乙数的
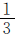，即甲数是乙数的
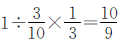,由此得出：两数的差30对应的是乙数的
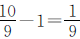,用甲、乙两数的差30除以
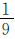就能求出乙数，再求甲数。
正确解答
解法一
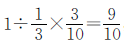
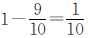
答：甲数是300，乙数是270。
方法点五 用条件转化法转化单位“1”
例10 某校四、五、六三个年级共有学生618人，其中五年级人数比四年级多10%，六年级人数比五年级少10%，求各年级各有学生多少人。
方法指导
把四年级人数看作单位“1”。五年级人数是四年级的1+10%＝110%；六年级人数比五年级少10%，即六年级人数是五年级人数的90%，所以六年级人数是四年级人数110%的90%，即110%×90%=99%。三个年级的总人数618人相当于四年级人数的（1+110%+99%）。先用四、五、六年级的总人数618除以（1+110%+99%）即可求出四年级的人数，再分别求五、六年级的人数。
正确解答
四年级人数：618÷[1+（1+10%）+（1+10%）×（1-10%）]
＝618÷309%
＝200（人）
五年级人数：200×（1+10%）＝220（人）
六年级人数：220×（1-10%）＝198（人）
答：四年级有200人，五年级有220人，六年级有198人。
例11 服装厂一车间人数占全厂总人数的 25%，二车间人数比一车间少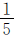
，三车间人数比二车间多
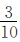，三车间是156人，这个服装厂一共有多少人?
方法指导
把全厂的人数看作单位“1”。一车间的人数占全厂人数的25%，二车间人数是全厂人数的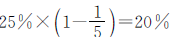
，三车间人数占全厂人数的
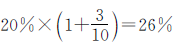，用三车间的156人除以它占全厂人数的分率26%就可以求出服装厂的总人数。
正确解答
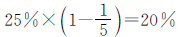
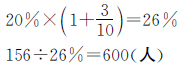
答：这个服装厂一共有600人。