第二章 转化法 - 第2讲 图形中的转化
方法概述
1．图形中的转化就是把不规则的平面图形或立体图形通过相减、分割、割补等方法，把不规则的图形转化成规则的几何图形，使需要解决的复杂问题变得简单化。
2．图形中的转化常用方法：
（1）相减法就是将所求的不规则图形的面积看成若干个规则的基本图形的面积之差。如本书第43页例1的题意分析图。
（2）分割法将不规则图形分割成若干个规则图形，然后分别计算各个图形的面积，最后相加求出整个图形的面积。如本书第45页例4的题意分析图。
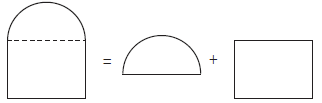
（3）割补法就是把原图形的一部分切割下来补在图形中的另一部分使之成为规则图形，从而使问题得到解决。如本书第45页例5的题意分析图。
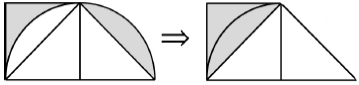
（4）重新组合法就是将不规则图形拆开，根据具体情况和计算的需要，重新组合成一个新的图形，设法求出这个新图形的面积。如本书第46页例8的题意分析图。
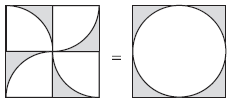
（5）对称添补法就是作出原图形的对称图形，从而得到一个新的规则图形，原来图形的面积就是这个新图形面积的一半。如本书第47页例10的题意分析图。
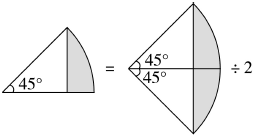
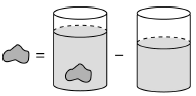
（6）排水法 就是将不规则的物体浸没到一个装有水的容器中，水面就会上升，上升的那部分水的体积就是不规则物体的体积。如本书第48页例11的题意分析图。
典例精讲
方法点一 运用相减法求图形面积
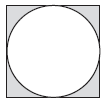
例1 已知正方形的边长是10厘米，在正方形内画一个最大的圆（如图）。求阴影部分的面积。
方法指导
本图是在正方形内画一个最大的圆，正方形的边长等于圆的直径，阴影部分的面积是用正方形的面积减去圆的面积。
正确解答
10×10-3.14×（10÷2）2=21.5（平方厘米）
答：阴影部分的面积是21.5平方厘米。
方法点二 运用分割法求图形面积
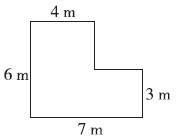
例2 下图是一个储藏室的平面图，要在这个储藏室的地面铺上地砖，铺地砖的面积是多少平方米？
方法指导
本题的分割方法不唯一，可以分成两个长方形，也可以分割成两个梯形。
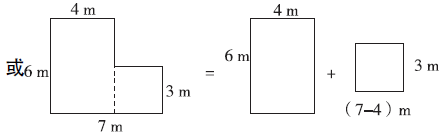
方法一 分割成两个长方形。其中一个长方形的长是4米，宽是（6-3）米，另一个长方形的长是7米，宽是3米，或一个长方形的长是6米，宽是4米，另一个长方形的长是（7-4）米，宽是3米（此时这个长方形是正方形）。
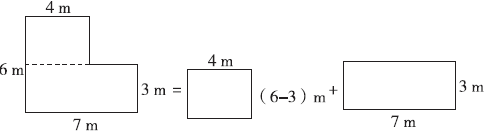
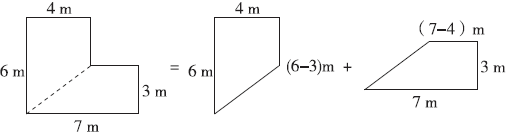
方法二 分割成两个梯形。其中一个梯形的上底是（6-3）米，下底是6米，高是4米，另一个梯形的上底是（7-4）米，下底是7米，高是3米。
正确解答
方法一 3×7+（6-3）×4=33（平方米）
或4×6+（7-4）×3=33（平方米）
方法二（6-3+6）×4÷2+（7-4+7）×3÷2=33（平方米）
答：铺地砖的面积是33平方米。
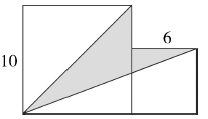
例3 大正方形的边长是10厘米，小正方形的边长是6厘米，求阴影部分的面积。
方法指导
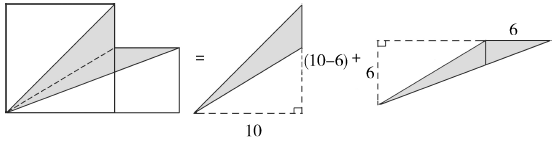
阴影部分是个不规则的图形，添加一条辅助线就可以将阴影部分分成两个三角形，一个三角形的底是（10-6）厘米，高是10厘米，另一个三角形的底和高都是6厘米。分别求出两个三角形的面积，然后将两个三角形的面积相加就可以求出阴影部分的面积。
正确解答
（10-6）×10÷2=20（平方厘米）
6×6÷2=18（平方厘米）
20+18=38（平方厘米）
答：阴影部分的面积是38平方厘米。
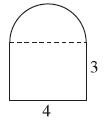
例4 下图是一个拱形门的平面图（拱形门上面是半圆形），现在要在这个拱形门的外面刷一层漆，算一算，刷漆的面积是多少？（单位：米）
方法指导
通过分割把这个图形分成一个直径为4米的半圆和一个长4米、宽3米的长方形，分别求出这两个图形的面积，然后把它们相加就是刷漆的面积。
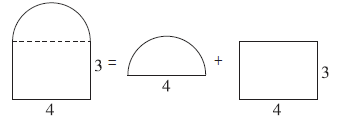
正确解答
4÷2=2（米）
3.14×22÷2=6.28（平方米）
4×3=12（平方米）
6.28+12=18.28（平方米）
答：刷漆的面积是18.28平方米。
方法点三 运用割补法求图形面积
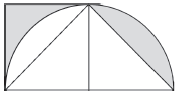
例5 正方形的边长是6分米，求阴影部分的面积。
方法指导
将图形右侧阴影部分割下来补到左侧，可得出阴影部分为三角形，求出阴影部分的面积。
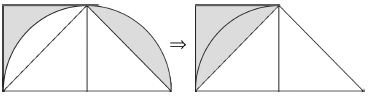
正确解答
6×6÷2=18（平方分米）
答:阴影部分的面积是18平方分米。
例6 长方形的长是6厘米，宽是3厘米，求阴影部分的面积。
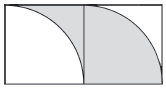
方法指导
将图形左侧阴影部分割下来通过平移补到右侧,组成一个新图形，新图形的阴影部分的面积等于原图形阴影部分的面积。
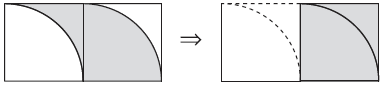
正确解答
3×3=9（平方厘米）
答：阴影部分的面积是9平方厘米。
方法点四 运用重新组合法求图形面积
例7 已知AB=BC=10厘米，三角形ACD是等腰直角三角形，求图中阴影部分的面积。
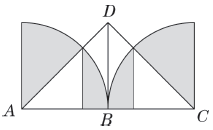
方法指导
沿BD将图形剪开，然后像图（2）重新组合。只要从半径为10厘米的半圆的面积中减去腰长为10厘米的等腰直角三角形的面积，就可以求出阴影部分的面积了。
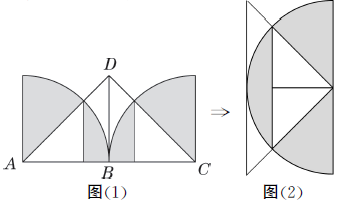
正确解答
3.14×102÷2=157（平方厘米）
10×10÷2=50（平方厘米）
157-50=107（平方厘米）
答：阴影部分的面积是107平方厘米。
例8 正方形的边长是8分米，求阴影部分的面积。
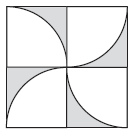
方法指导
把大正方形剪成4个大小形状相同的正方形，然后重新组合成新的图形，阴影部分的面积就是大正方形的面积减去该正方形内最大圆的面积，这样就把复杂问题简单化了。
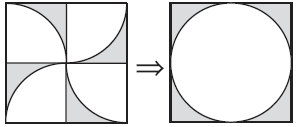
正确解答
8×8-3.14×（8÷2）2=13.76（平方分米）
答：阴影部分的面积是13.76平方分米。
例9 正方形ABCD的边长为4米，分别以B、D为圆心、4米为半径在正方形内画圆，求阴影部分的面积。
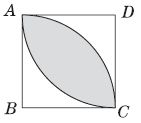
方法指导
该图形可以按两个相同的扇形重新组合进行思考，这两个扇形组合成一个正方形后，阴影部分是多出的部分，所以它的面积就等于两个扇形的面积减去正方形的面积。
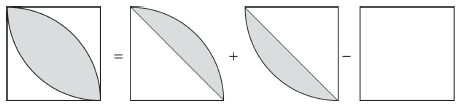
正确解答
3.14×42÷4×2-4×4=9.12（平方米）
答：阴影部分的面积是9.12平方米。
方法点五 运用对称添补法求图形面积
例10 已知圆的半径是10厘米，求阴影部分的面积。
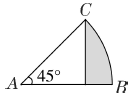
方法指导
以AB边所在直线为对称轴添补一个同样大的图形，重新组成一个新图形。用减法求出新图形阴影部分的面积后再除以2就得出原图形的阴影部分的面积。
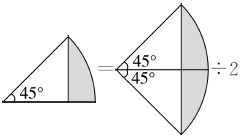
正确解答
（3.14×102÷4-10×10÷2）÷2=14.25（平方厘米）
答：阴影部分的面积是14.25平方厘米。
方法点六 运用排水法求物体体积
例11 一个底面直径为10厘米的圆柱形容器中装有一部分水，水中放着一个底面直径为8厘米，高为9厘米的圆锥形铁块（铁块完全浸没水中），把这个铁块从水中取出后，容器里的水将下降几厘米？
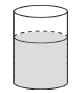
方法指导
理解题意可知，圆锥形铁块的体积就等于下降的那部分水的体积。先求出圆锥形铁块的体积，再除以圆柱形容器的底面积，所求即是容器里的水下降的高度。
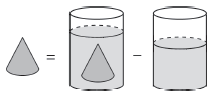
正确解答
圆锥形铁块的体积：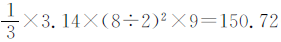
（立方厘米）
圆柱形容器的底面积:3.14×（10÷2）2=78.5（平方厘米）
下降的高度：150.72÷78.5=1.92（厘米）
答：容器里的水将下降1.92厘米。