第二章 转化法 - 第1讲 计算中的转化
方法概述
1.计算中的转化是指通过运算性质、运算定律、运算公式的运用，实现简化算式，提高运算的速度和运算的准确性。
2.计算中的转化的方法。
（1）运用运算性质、运算定律转化。
例 237+621-321+163
=（237+163）+（621-321）
=400+300
=700
（2）运用分组计算的方法转化。
例 100+99-98-97+96+95-94-93+…+4+3-2-1
=（100+99-98-97）+（96+95-94-93）+…+（4+3-2-1）
=4+4+4+…+4
=4×25
=100
（3）运用运算公式转化。
例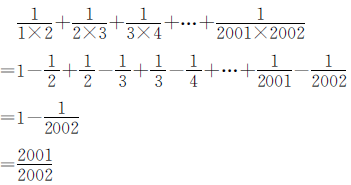 
典例精讲
方法点一 运用运算性质、运算定律进行转化
例1 883+（117-68）
方法指导
根据加法的运算性质，去掉算式中的括号，然后先计算883+117，再用所得的和减去68。
正确解答
883+（117-68）
=883+117-68
=1000-68
=932
例2 1300÷25
方法指导
本题可以运用商不变的性质简算。被除数和除数同时扩大4倍，除数25扩大4倍后得到一个整百数，这样原式就转化为“（1300×4）÷（25×4）”。
正确解答
1300÷25
=（1300×4）÷（25×4）
=5200÷100
=52
例3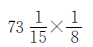
方法指导
本题可以应用乘法分配律进行简算。先把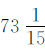
拆分成
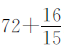的形式，再计算。
正确解答
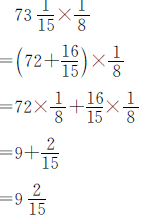
例4 2×5×4×25×8×125
方法指导
根据乘法交换律和乘法结合律可以把原式进行转化。原式=（2×5）×（4×25）×（8×125）。
正确解答
2×5×4×25×8×125
=（2×5）×（4×25）×（8×125）
=10×100×1000
=1000000
例5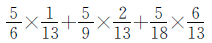 
方法指导
本题可以根据乘法分配律进行转化。先把本题转化为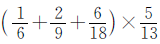
的形式，再计算。
正确解答
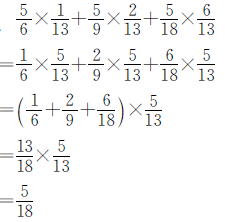
例6 99999×99999
方法指导
本题可以应用乘法分配律简算。99999接近100000，所以先把99999看作是（100000-1）,然后根据乘法分配律计算。
正确解答
99999×99999
=99999×（100000-1）
=99999×100000-99999×1
=9999900000-99999
=9999800001
例7 3333×3333+3333×6667
方法指导
本题可以应用提取公因数（即乘法分配律的逆运算）的方法进行转化凑整，两个乘法算式中都有3333，根据提取公因数的方法，原式=3333×（3333+6667）。
正确解答
3333×3333+3333×6667
=3333×（3333+6667）
=3333×10000
=33330000
例8 2772÷28+34965÷35
方法指导
本题可以先凑整，再应用（A+B）÷C=A÷C+B÷C进行简算。2772可以看作是（2800-28）,34965可以看作是（35000-35），原式转化为（2800-28）÷28+（35000-35）÷35，然后进行简算。
正确解答
2772÷28+34965÷35
=（2800-28）÷28+（35000-35）÷35
=2800÷28-28÷28+35000÷35-35÷35
=100-1+1000-1
=1098
例9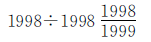 
方法指导
被除数是1998，除数是一个带分数，且整数部分和分数部分的分子都是1998。可以把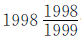
化成假分数，再把分子转化成两个数相乘的形式，便于约分和计算。
正确解答
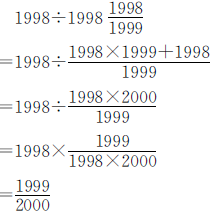
例10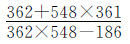 
方法指导
仔细观察分子、分母中各数的特点就会发现，分母中的被减数362×548可以化成（361+1）×548＝361×548+548，同时发现548－186＝362，所以分母可以化成361×548+362的形式，分子、分母完全相同，可以进行约分。
正确解答
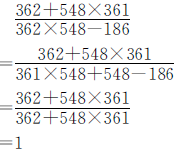
方法点二 运用分组计算的方法转化
例11 100+99-98-97+96+95-94-93+…+4+3-2-1
方法指导
方法一 根据运算符号出现的规律分组。把原式中的100个数按照运算符号出现的规律，每4个数分为一组，每组里的结果都等于4，一共可以分成25组，这组算式的结果就是25个4的和。
方法二 此题也可以通过前后次序的交换，把两个数结合成一组，一共可以结合成50组，每组值均为2，这组算式的结果就是50个2的和。
正确解答
方法一 100+99-98-97+96+95-94-93+…+4+3-2-1
=（100+99-98-97）+（96+95-94-93）+…+（4+3-2-1）
=4+4+4+…+4
=4×25
=100
方法二 100+99-98-97+96+95-94-93+…+4+3-2-1
=（100-98）+（99-97）+（96-94）+（95-93）+…+（4-2）+（3-1）
=2×50
=100
例12 1+2+3+4+5+6+…+99+100
方法指导
观察这组算式，发现1+100=2+99=3+98=4+97=…=50+51=101 ，100个数可以分成50组，这组算式的结果就是101×50的积。
正确解答
1+2+3+4+5+6+…+99+100
=（1+100）×（100÷2）
=101×50
=5050
方法点三 运用拆项公式转化
例13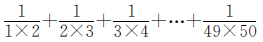 
方法指导
因为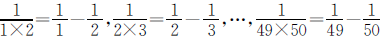
,所以此题可以通过拆项的方法，使得其中一部分分数相互抵消，从而简化计算过程。
正确解答
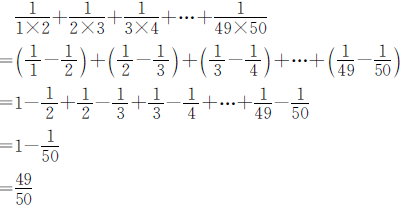
例14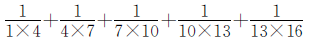 
方法指导
观察分母可以发现该式是有序排列的,1X4,4x7,7x10……
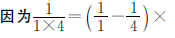
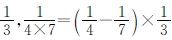
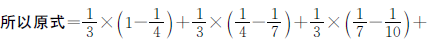
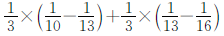
正确解答
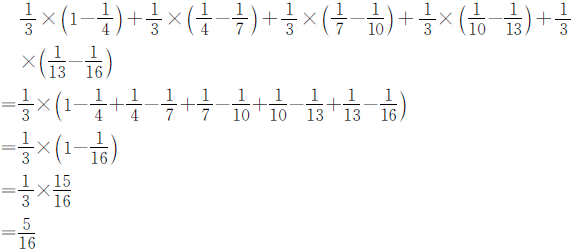
例15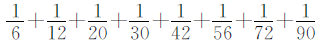 
方法指导
算式中
,这样原式就可以转化成
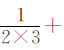
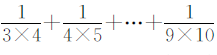，从而进行简算。
正确解答
