第一章 图示法 - 第4讲 画集合图法
方法概述
1.集合图法就是借助集合图列举某一确定范围内的事物,根据集合间的重叠关系解决问题的方法。 如本书第30页例4的题意分析图。
2.画集合图法解题的一般步骤:
(1)用集合图表示出题中的数量;
(2)确定集合之间的关系,标出重叠部分;
(3)运用集合间包含或排除的关系解决问题。
典例精讲
方法点一 画集合图解两个集合的重叠问题
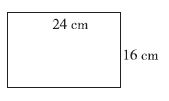
例1 把下面的长方形纸分割成边长是整厘米数的正方形,正方形的边长可以是多少厘米?最长是多少厘米?
方法指导
要把长方形纸分割成正方形,则正方形的边长一定是24和16公有的因数,即公因数。用集合图分别表示出24和16的因数(如图一),由两个集合的共同部分可以确定公因数(如图二),进而求出最大公因数。
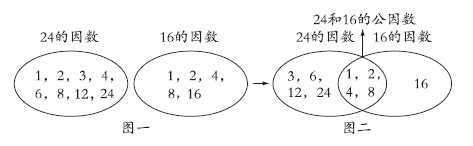
1,2,4,8是24和16的公因数,填写在两个集合的相交处。
正确解答
正方形的边长可以是1厘米、2厘米、4厘米、8厘米;边长最长是8厘米。
总结:把两个数的因数分别看作一个集合,它们的公因数就是这两个集合的重叠部分。
例2 学校甬路旁栽了一行小树,从第一棵到最后一棵的距离是80 m。原来每隔2 m栽一棵树,现在小树长大了,改为每隔5 m栽一棵树。如果两端的树不移动,中间有几棵树不用移动?
方法指导
树的间隔由2 m改为5 m,则位于2和5公倍数位置上的树不用移动。2和5的公倍数可以用下面的集合图表示。
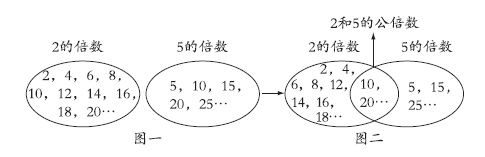
把2的倍数写在一个集合里,5的倍数写在另一个集合里(如图一),两个集合相交的部分就是2和5的公倍数(如图二)。
正确解答
在80以内,2和5的公倍数有10,20,30,…,70,共有7个数,表示在这7个位置上的树不用移动,所以中间有7棵树不用移动。
例3 三年级一班有38人,订阅《语文报》的有27人,订阅《数学报》的有22人。这个班级每人至少订阅了一种报刊,订阅两种报刊的有多少人?
方法指导
由题意可知,订阅《语文报》的27人中有一部分人还订阅了《数学报》,订阅《数学报》的22人中也有一部分人订阅了《语文报》。所以,如果用A圈表示订阅《语文报》的人数,用B圈表示订阅《数学报》的人数,则两个圈相交的部分就表示同时订阅两种报刊的人数(如图所示)。
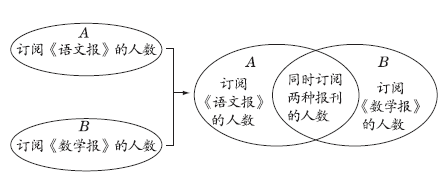
从图中可以看出,订阅两种报刊的人数等于A圈的人数加上B圈的人数减去全班的总人数。
正确解答
27+22-38=11(人)
答:订阅两种报刊的有11人。
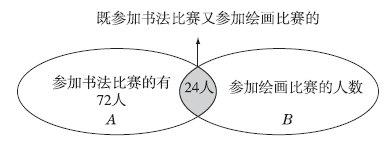
例4 实验小学有110名学生参加书法和绘画比赛,参加书法比赛的有72人,既参加书法比赛又参加绘画比赛的有24人。参加绘画比赛的有多少人?(三年级)
方法指导
题中信息可以用下面的集合图表示:
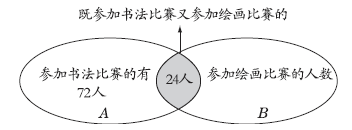
A圈表示参加书法比赛的人数,B圈表示参加绘画比赛的人数,两圈相交的阴影部分表示既参加书法比赛又参加绘画比赛的人数。由图可知,参加绘画比赛的人数应等于总人数减去只参加书法比赛的人数。而只参加书法比赛的人数等于A圈的人数减去阴影部分的人数。
正确解答
只参加书法比赛的人数:
72-24=48(人)
参加绘画比赛的人数:
110-48=62(人)
答:参加绘画比赛的有62人。
总结:集合的重叠部分同时属于这两个集合。计数时,每个集合都可以看作独有部分与重叠部分的和。
方法点二 画集合图解多个集合的重叠问题
例5 某班有45名学生。据统计,喜爱足球、篮球、排球这三项运动的各有26人,喜爱其中两项运动的分别有13、14、15人。三项运动都喜爱的有多少人?
方法指导
用A圈表示喜爱足球的人数,B圈表示喜爱篮球的人数,C圈表示喜爱排球的人数。则A、B两圈相交的部分表示既喜爱足球又喜爱篮球的人数;B、C两圈相交的部分表示既喜爱篮球又喜爱排球的人数;A、C两圈相交的部分表示既喜爱足球又喜爱排球的人数;A、B、C三个圈相交的部分表示三项运动都喜爱的人数(如图所示)。
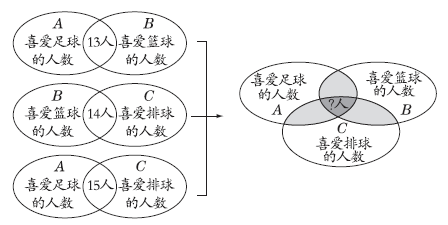
由题意可知,3个圈各有26人,但班级总人数只有45人,所以重叠部分人数应为26×3-45=33(人)。但有一些同学同时喜爱这三项球类运动,所以又出现了再次重叠,用喜爱两项运动的人数减去33人,即为喜爱三项运动的人数。
正确解答
喜爱两项运动以上的人数:
26×3-45=33(人)
只喜爱两项运动的人数:
13+14+15=42(人)
喜爱三项运动的人数:
42-33=9(人)
答:三项运动都喜爱的有9人。
提示:解决三个集合的重叠问题,每两个集合都有重叠的部分,且有一个重叠部分经过了两次重叠。
例6 某工作组中有6人会说英语,5人会说法语,5人会说西班牙语,有3人既会说英语又会说法语,有2人既会说法语又会说西班牙语,有2人既会说西班牙语又会说英语,有1人这三种语言都会说。这个工作组一共有几人?
方法指导
题中的数量关系可以用下面的集合图表示。
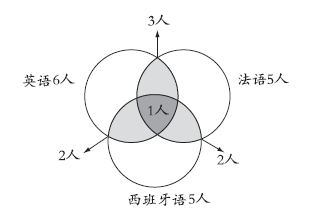
由上图可知,如果把会任一种语言的人数相加,总数是6+5+5=16(人)。会两种以上语言的人数是3+2+2=7(人),但7人中的1人同时会三种语言,再次重叠,所以重叠部分实际上是7-1=6(人)。工作组的人数可以用总数量减去重叠部分的数量。
正确解答
总数量:6+5+5=16(人)
会两种以上语言的人数:3+2+2-1=6(人)
工作组人数:16-6=10(人)
答:这个工作组一共有10人。
提示:集合总数量=所有集合数量和-重叠数量。